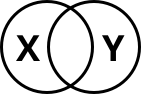
Syllogismen: Eine kurze Einführung

Syllogismen sind eine Form der deduktiven Argumentation, bei der man zu einer bestimmten Schlussfolgerung gelangt, indem man zwei sich unterscheidende Aussagen (Prämissen) betrachtet.[1]

Form

Ein Syllogismus besteht aus drei Bestandteilen.

  1. Hauptprämisse
  2. Nebenprämisse
  3. Schlussfolgerung
Beispiel
  1. Kein Rechteck ist ein Kreis.
  2. Alle Quadrate sind Rechtecke.
    Es folgt: Einige Quadrate sind keine Kreise.

Wie sich zeigt, stellen Syllogismen ein relativ klares und einfaches Mittel dar, um ein Argument vorzubringen. Ein Syllogismus unterliegt folgender Struktur bzw. Formatierung:

Prädikat & Subjekt

Im kategorischen Syllogismus sind Prämissen und Konklusion kategorische Urteile, d. h. Aussagen, in denen einem Begriff, dem Subjekt, ein anderer Begriff, das Prädikat, in bestimmter Weise zu- oder abgesprochen wird.

Beispiel
  1. Keine Nesseltiere (Subjekt) sind Wirbeltiere (Prädikat).
  2. Alle Quallen sind Nesseltiere.
    Es folgt: Keine Quallen sind Wirbeltiere.

Im obigen Beispiel wird dem Subjekt “Nesseltiere” das Prädikat “Wirbeltiere” abgesprochen.

Mittelbegriff

Der Mittelbegriff ist dabei stets der Begriff, der in beiden Prämissen erscheint[2]. Es ist das gemeinsame Element, das die Haupt- und Nebenprämisse verbindet.

Beispiel
  1. Kein Rechteck (Mittelbegriff) ist ein Kreis (Prädikat).
  2. Alle Quadrate (Subjekt) sind Rechtecke (Mittelbegiff).
    Es folgt: Einige Quadrate (Subjekt) sind keine Kreise (Prädikat).

Schlussfolgerung

Die Schlussfolgerung (auch Konklusion genannt) eines gültigen Syllogismus enthält stets Subjekt und Prädikat. Wird die erste Prämisse mit der zweiten Prämisse vertauscht, findet sich das Prädikat vor dem Subjekt.

Beispiel
  1. Kein Säugetier (Mittelbegriff) ist ein Kiemenatmer (Prädikat).
  2. Einige Wassertiere (Subjekt) sind Säugetiere (Mittelbegriff).
    Es folgt: Einige Wassertiere (Subjekt) sind Kiemenatmer (Prädikat).

Urteil der Schlussfolgerung

Die Prämissen und Schlussfolgerungen eines Syllogismus können jeweils einem von vier Typen entsprechen, die mit den Buchstaben A, E, I und O wie folgt bezeichnet werden. Die Bedeutung der Buchstaben wird in der Tabelle dargestellt:

Code Quantor (bsp.) Subjekt Kopula (bsp.) Prädikat Typ Beispiel
A Alle S sind P universell bejahend Alle Fische sind Wirbeltiere.
E Keine S sind P universell verneinend Keine Menschen sind Fische.
I Einige S sind P teilweise bejahend Einige Menschen sind Frauen.
O Einige S sind keine P teilweise verneinend Einige Menschen sind keine Frauen.

Distribution

Ein Begriff gilt innerhalb einer syllogistischen Aussage als distribuiert, wenn er sich innerhalb der Aussage auf alle Gegenstände bezieht, auf die der Begriff zutrifft und dieser durch jeden gültigen Unterbegriff seiner selbst ersetzbar ist.[3] Nicht distribuiert ist das Vorkommen eines Begriffs in einer Aussage, wenn die Aussage keinen solchen Schluss zulässt.

Code Subjekt Prädikat
A distribuiert -
E distribuiert distribuiert
I - -
O - distribuiert

Beispiel

Aus “Alle Beamten sind Menschen” folgt, dass ein Beamter ein Mensch ist. Aber es folgt nicht, dass jeder Mensch ein Beamter ist. Widerrum lassen sich aus dem nicht distributierten Begriff “Menschen” keine Unterbegriffe des Subjekts (“Beamte”) ableiten. So lässt sich aus der Tatsache, dass “alle Beamten sind Menschen” sind, mitnichten für den Unterbegriff (“Zöllner”) folgern, dass alle Beamte Zöllner sind.

Position der Begriffe (Figur)

Die unterschiedlichen Positionen des Prpädikats, Subjekts und Mittelbegriffs führen zu einer weiteren Klassifizierung von Syllogismen, die als Figuren bezeichnet werden. In jeder Figur lassen sich gültige Schlüsse ziehen.[4]

1. Figur 2. Figur 3. Figur 4. Figur
1. Prämisse Mittelbegriff – Prädikat Prädikat – Mittelbegriff Mittelbegriff – Prädikat Prädikat – Mittelbegriff
2. Prämisse Subjekt – Mittelbegriff Subjekt – Mittelbegriff Mittelbegriff – Subjekt Mittelbegriff – Subjekt
Konklusion Subjekt - Prädikat Subjekt - Prädikat Subjekt - Prädikat Subjekt - Prädikat

Regeln der Gültigkeit

Für einen kategorischen Syllogismus gibt es die folgenden grundsätzlichen Regeln:

Qualität

  1. Der Mittelbegriff darf nicht in der Schlussfolgerung vorhanden sein. [5]
  2. Mindestens eine Prämisse muss eine bejahende Aussage sein.[5]
  3. Wenn beide Prämissen bejahend sind, dann muss auch die Schlussfolgerung bejahend sein.[5]
  4. Wenn eine der beiden Prämissen verneinend ist, dann muss auch die Konklusion verneinend sein.[5]

Quantität

  1. Mindestens eine der beiden Prämissen muss eine allgemeine Aussage sein.[5]
  2. Wenn eine der beiden Prämissen eine teilweise Aussage ist, kann die Schlussfolgerung keine allgemeine Aussage sein.[5]

Distribution

  1. Der Mittelbegriff muss mindestens einmal distibutiert vorkommen.[3]
  2. Wenn ein Begriff in der Konklusion distributiert auftritt, muss er auch in einer Prämisse distributiert auftreten.[3]

Übersicht der kategorisch gültigen Syllogismen

Von den 256 möglichen Kombinationen sind insgesamt nur 24 gültig.[6] Diese werden unterschieden in schwache und starke Modi.[7]

Was ist ein schwacher Syllogismus?

Die Schlussfolgerung eines schwachen Modi behauptet weniger als sich auf den Prämissen hätte folgern lassen. So ergibt sich, dass aus jedem Syllogismus, dessen Schlussfolgerung ein universelles Urteil erlaubt (A, E), sich ein schwacher Modus ableiten lässt, indem die Schlussfolgerung ein partikuläres Urteil ist (I, O).[8]

Übersicht

1. Figur

Figur Merkwort Urteile Typ
1 Barbara A A A stark
1 Barbari A A I schwach
1 Celarent E A E stark
1 Celaront E A O schwach
1 Darii A I I stark
1 Ferio E I O stark

2. Figur

Figur Merkwort Urteile Typ
2 Camestres A E E stark
2 Camestrop A E O schwach
2 Cesare E A E stark
2 Cesaro E A O schwach
2 Baroco A O O stark
2 Festino E I O stark

3. Figur

Figur Merkwort Urteile Typ
3 Darapti A A I stark
3 Felapton E A O stark
3 Bocardo O A O stark
3 Datisi A I I stark
3 Disamis I A I stark
3 Ferison E I O stark

4. Figur

Figur Merkwort Urteile Typ
4 Bamalip A A I stark
4 Calemes A E E stark
4 Calemop A E O schwach
4 Fesapo E A O stark
4 Dimatis I A I stark
4 Fresison E I O stark

Aufzeigem der logischen Gültigkeit mittels Diagrammen

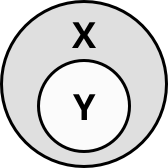
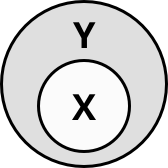
Besonders einfach und übersichtlich kann man die 4 Urteilsarten durch Euler-Diagramme interpretieren:[9]

Eueler-Diagramme

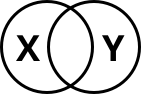Urteil Abbildung des Euler-Diagramm Abbildung des Euler-Diagramm Abbildung des Euler-Diagramm Abbildung des Euler-Diagramm
A x
I x x x
O x x x
E x

Beispiel

  1. Keine Vögel (Mittelbegriff) sind ein Säugetier (Prädikat).
  2. Alle Adler (Subjekt) sind Vögel (Mittelbegriff).
    Es folgt: Einige Adler (Subjekt) sind keine Säugetiere (Prädikat).

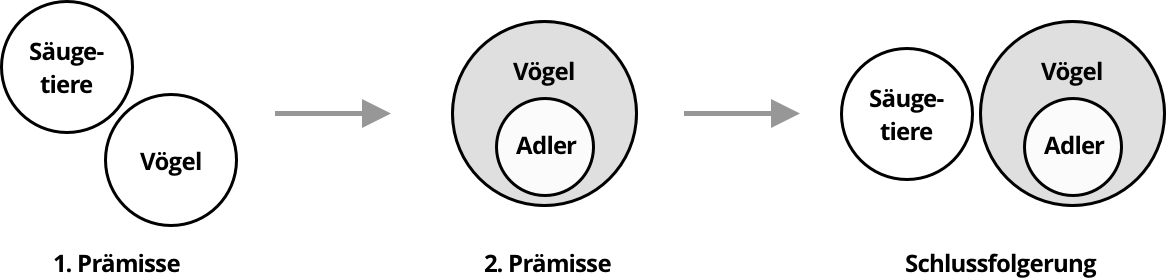
Abbildung des Euler-Diagramm

Venn-Diagramme

Gegenüber Euler-Diagrammen stellen Venn-Diagramme eine methodische Weiterentwicklung dar, um Syllogismen visuell zu veranschaulischen und zu validieren. Ein Venn-Diagramm besteht aus überlappenden Kreisen, die die Zusammenhänge der Aussagen darstellen. Die Überschneidung der Kreise ergibt jeweils eine Teilmenge.[10]

Beispiel

  1. Alle Vögel sind Wirbeltiere.
  2. Einige Tiere sind keine Wirbeltiere.
    Es folgt: Einige Tiere sind keine Vögel.

Abbildung des Venn-Diagramm

Beispiel

  1. Alle Vögel sind Wirbeltiere.
  2. Alle Wirbeltiere sind Lebenwesen.
    Es folgt: Einige Lebenwesen sind Vögel.

Abbildung des Venn-Diagramm

Konditioneller Syllogismus

Bedingte Syllogismen folgen einem “Wenn A wahr ist, dann ist B wahr”-Muster der Logik.[11] Man könnte Sie auch als hypothetische Syllogismen bezeichnen, deren Schlüsse nicht immer gültig sind, bzw. nur einer subjektiven Wahrheit folgen.

Beispiel:

  1. Wenn der Klimawandel sich manifestiert, wird es mehr Regnen.
  2. Wenn es mehr regnet, kommt es zu Überschwemmungen.
    Es folgt: Wenn der Klimawandel sich manifestiert, dann gibt es Überschwemmungen.

Disjunkter Syllogismus

Disjunktive Syllogismen folgen der Prämisse “Wenn A wahr ist, muss B falsch sein”. Sie sagen nicht aus, ob eine Haupt- oder Nebenprämisse richtig ist. Aber es ist klar, dass eine davon richtig ist.

Beispiel:

  1. Entweder scheint die Sonne oder es regnet.
  2. Es regnet.
    Schlussfolgerung: Die Sonne scheint nicht.

Referenzen

  1. Joachim Lege, Pragmatismus und Jurisprudenz: über die Philosophie des Charles Sanders Peirce und über das Verhältnis von Logik, Wertung und Kreativität im Recht, Mohr Siebeck, 1999, S.83 ↩

  2. G. Patzig, Übersetzt von Jonathan Barnes, Aristotle’s Theory of the Syllogism: A Logico-Philological Study of Book A of the Prior Analytics, Band 16 von Synthese Library, Springer Science & Business Media, 2013, S. 116 ↩

  3. Gert Ueding, Gregor Kalivoda, St - Z, Band 9 von Ueding, Gert: Historisches Wörterbuch der Rhetorik, Walter de Gruyter, 2012, S. 272 ↩ ↩ ↩

  4. Thomas Zoglauer, Einführung in die formale Logik für Philosophen, UTB, 2016, S.95 ↩

  5. Christian Weiss, Lehrbuch der Logik: nebst einer Einleitung zur Philosophie überhaupt und besonders zu der bisherigen Metaphysik, Göschen, 1801, S.133 - 134 ↩ ↩ ↩ ↩ ↩ ↩

  6. Paul Lorenzen, Formale Logik: Band 1176 von Sammlung Göschen, Walter de Gruyter, 2011, S. 25 ↩

  7. Jürgen Mittelstraß, Enzyklopädie Philosophie und Wissenschaftstheorie: Band 4: Sp - Z, Springer-Verlag, 2017, S. 157 ↩

  8. Timm Lampert, Klassische Logik: Einführung mit interaktiven Übungen, Walter de Gruyter, 2013 ↩

  9. Werner Herkner, Psychologie, Springer-Verlag, 2013, S. 176 ↩

  10. Paul Walter, Kritisch denken – treffend argumentieren, Springer-Verlag 2016, Petra Wenzl S.11 ↩

  11. Lothar Kolmer, Carmen Rob-Santer, Studienbuch Rhetorik, Band 2335 von Rhesis. Arbeiten zur Rhetorik und ihrer Geschichte, UTB, 2008, S.160 ↩